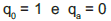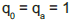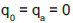Considere o clássico problema da ruína do jogador A que, em cada etapa do jogo, tem probabilidade p de vencer e ganhar uma unidade do capital de seu adversário, cuja probabilidade de vencer é q = 1 - p. As etapas do jogo são independentes, o capital inicial de A é igual a z, e o de B é igual a a-z. O jogo termina quando um dos jogadores se arruína. A probabilidade qz de ruína do jogador A pode ser obtida através da solução de uma equação de diferenças finitas de segunda ordem da forma
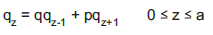
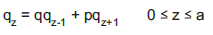
A solução desta equação envolverá duas constantes, que serão determinadas a partir da consideração de dois valores iniciais da função qz, que são